Written by Paul Bourke
December 1993
A platonic solid (also called regular polyhedra) is a convex polyhedron
whose vertices and faces are all of
the same type.
In two dimensions there are an infinite number of regular polygons.
In three dimensions there are just five regular polyhedra.
-
Tetrahedron - made of 4 equilateral triangles
-
Cube - made of 6 squares
-
Octahedron - made of 8 equilateral triangles
-
Dodecahedron - made of 12 regular pentagons
-
Icoshedron - made of 20 equilateral triangles
In 4 dimensions there are 6 regular polytopes
-
4 simplex - made of 5 tetrahedra, 3 meeting at an edge
-
Hypercube - made of 8 cubes, 3 meeting at an edge
-
16 cell - made of 16 tetrahedra, 4 meeting at an edge
-
24 cell - made of 24 octahredra, 3 meeting at an edge
-
120 cell - 120 dodecahedra, 3 meeting at an edge
-
600 cell - 600 tetrahedra, 5 meeting at an edge
The measured properties of the 3 dimensional regular polyhedra

|
Tetrahedron
Vertices: 4
Edges: 6
Faces: 4
Edges per face: 3
Edges per vertex: 3
Sin of angle at edge: 2 * sqrt(2) / 3
Surface area: sqrt(3) * edgelength^2
Volume: sqrt(2) / 12 * edgelength^3
Circumscribed radius: sqrt(6) / 4 * edgelength
Inscribed radius: sqrt(6) / 12 * edgelength |

|
Octahedron
Vertices: 6
Edges: 12
Faces: 8
Edges per face:3
Edges per vertex: 4
Sin of angle at edge: 2 * sqrt(2) / 3
Surface area: 2 * sqrt(3) * edgelength^2
Volume: sqrt(2) / 3 * edgelength^3
Circumscribed radius: sqrt(2) / 2 * edgelength
Inscribed radius: sqrt(6) / 6 * edgelength |

|
Hexahedron
(cube)
Vertices: 8
Edges: 12
Faces: 6
Edges per face: 4
Edges per vertex: 3
Sin of angle at edge: 1
Surface area: 6 * edgelength^2
Volume: edgelength^3
Circumscribed radius: sqrt(3) / 2 * edgelength
Inscribed radius: 1 / 2 * edgelength |

|
Icosahedron
Vertices: 12
Edges: 30
Faces: 20
Edges per face: 3
Edges per vertex: 5
Sin of angle at edge: 2 / 3
Surface area: 5 * sqrt(3) * edgelength^2
Volume: 5 * sqrt(3 + sqrt(5)) / 12 * edgelength^3
Circumscribed radius: sqrt(10 + 2 * sqrt(5)) / 4 * edgelength
Inscribed radius: sqrt(42 + 18 * sqrt(5)) / 12 * edgelength |

|
Dodecahedron
Vertices: 20
Edges: 30
Faces: 12
Edges per face: 5
Edges per vertex: 3
Sin of angle at edge: 2 * sqrt(5)
Surface area: 3 * sqrt(25 + 10 * sqrt(5)) * edgelength^2
Volume: sqrt(15 + 7 * sqrt(5)) / 4 * edgelength^3
Circumscribed radius: sqrt(sqrt(15) + sqrt(3)) / 4 * edgelength
Inscribed radius: sqrt(250 + 110 * sqrt(5)) / 20 * edgelength |
"Standardised" coordinates for
the platonic solids
The solids as drawn in Kepler's Mysterium Cosmographicum
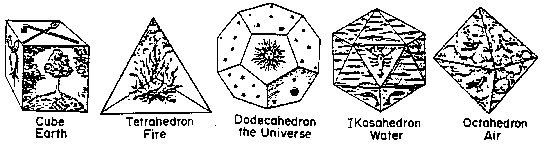
and represented in stone from a neolythic settlement
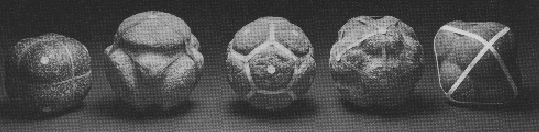
Subject:
Re: Platonic
Solids, intersection of three cylinders
Date:
Tue, 20 Oct
1998 08:32:24 +1000
From:
Paul Bourke
<pdb@mhri.edu.au>
To:
david.Boeno@wanadoo.fr
>For my next art shows I would like to present some images of Euclidean
>manuscripts with links to your pages : "Platonic Solids", "intersection
of
>three cylinders"
>For instance, the first step, in Ecole des Beaux Arts de Dijon, on
november
>98, will be on a offline way.
>A CD rom for inside use will be made at this occasion.
>So, would you please tell me if you agree.
>Of course, the copyright of your web pages will appear.
I have no objection to material from my WWW pages being
used as long
as appropriate credit is given. If you end up putting
anything online
I'd like to see it.
---------------------------------------------------------------------
Paul Bourke
pdb@mhri.edu.au
Brain Dynamics Research Unit
http://www.mhri.edu.au/bdl/
Mental Health Research Institute
Ph: 61 3 9389 2602
Locked Bag 11, Parkville
Fax: 61 3 9387 5061
Victoria 3052, Australia