
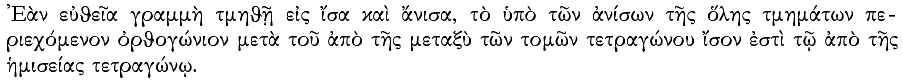









|





Si recta linea per equalia atque inequalia secetur, quod sub inequalibus tocius sectionis rectangulum continetur,
cum eo quadrato quod inter utrasque est sectiones,
equum est ei quadrato quod ab ea describitur
que tocius linee per equalem et inequalem divisionem secte medietatem optinere cognoscitur.
 
 |











