English Word and Phrase Searche-mail us problems and
comments | copyright statement
21) Euclid Elements 13.8 (Heath)
If in an equilateral and equiangular pentagon
straight lines subtend two angles taken in order, they cut one another
in extreme and mean ratio, and their greater segments are equal
to the side of the pentagon.
For in the equilateral and equiangular pentagonABCDE
let the straight lines AC, BE, cutting one another at the
point H, subtend two angles taken in order, the angles at
A,
B;
I say that each of them has been cut in extreme and mean ratio at the point
H,
and their greater segments are equal to the side of the pentagon. 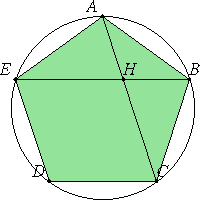
For let the circle ABCDE be circumscribed about the pentagonABCDE.
[[IV. 14]]
Then, since the two straight lines EA, AB are equal to
the two AB, BC, and they contain equal angles, therefore
the base BE is equal to the base AC, the triangle ABE
is equal to the triangle ABC, and the remaining angles will be equal
to the remaining angles respectively, namely those which the equal sides
subtend. [[I. 4]]
Therefore the angle BAC is equal to the angle ABE; therefore
the angle AHE is double of the angle BAH. [[I.
32]]
But the angle EAC is also double of the angle BAC, inasmuch
as the circumference EDC is also double of the circumference CB;
[[III. 28], [VI. 33]] therefore
the angle HAE is equal to the angle AHE; hence the straight
line HE is also equal to EA, that is, to AB. [[I.
6]]
And, since the straight line BA is equal to AE, the angle
ABE
is also equal to the angle AEB. [[I. 5]]
But the angle ABE was proved equal to the angle BAH;
therefore the angle BEA is also equal to the angle BAH.
And the angle ABE is common to the two triangles ABE
and ABH; therefore the remaining angle BAE is equal to the
remaining angle AHB; [[I. 32]] therefore the triangle
ABE
is equiangular with the triangle ABH; therefore, proportionally,
as EB is to BA, so is AB to BH. [[VI.
4]]
But BA is equal to EH; therefore, as BE is to
EH,
so is EH to HB.
And BE is greater than EH; therefore EH is also
greater than HB. [[V. 14]]
Therefore BE has been cut in extreme and mean ratio at H,
and the greater segment HE is equal to the side of the pentagon.
Similarly we can prove that AC has also been cut in extreme
and mean ratio at H, and its greater segment CH is equal
to the side of the pentagon. Q.
E. D.
Euclid Elements 13.10 (Heath)
Illustrations courtesy of David E. Joyce
If an equilateral pentagon be
inscribed in a circle, the square on the side of the pentagon
is equal to the squares on the side of the hexagon and on that of the decagon
inscribed in the same circle.
Let ABCDE be a circle, and let the equilateral pentagonABCDE
be inscribed in the circle ABCDE.
I say that the square on the side of the pentagonABCDE
is equal to the squares on the side of the hexagon and on that of the decagon
inscribed in the circle ABCDE.
For let the centre of the circle, the point F, be taken, let
AF
be joined and carried through to the point G, let FB be joined,
let FH be drawn from F perpendicular to AB and be
carried through to K, let AK, KB be joined, let FL
be again drawn from F perpendicular to AK, and be carried
through to M, and let KN be joined.
Since the circumference ABCG is equal to the circumference AEDG,
and in them ABC is equal to AED, therefore the remainder,
the circumference CG, is equal to the remainder GD. 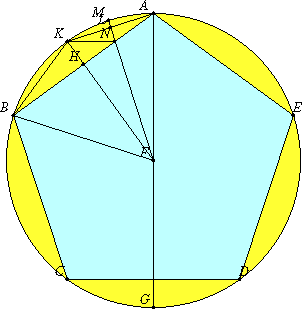
But CD belongs to a pentagon;
therefore
CG belongs to a decagon.
And, since FA is equal to FB, and FH is perpendicular,
therefore the angle AFK is also equal to the angle KFB. [[I.
5], [I. 26]]
Hence the circumference AK is also equal to KB; [[III.
26]] therefore the circumference AB is double of the circumference
BK;
therefore the straight line AK is a side of a decagon.
For the same reason AK is also double of KM.
Now, since the circumference AB is double of the circumference
BK,
while the circumference CD is equal to the circumference
AB,
therefore the circumference CD is also double of the circumference
BK.
But the circumference CD is also double of CG; therefore
the circumference CG is equal to the circumference BK.
But BK is double of KM, since KA is so also; therefore
CG
is also double of KM.
But, further, the circumference CB is also double of the circumference
BK,
for the circumference CB is equal to BA.
Therefore the whole circumference GB is also double of BM;
hence the angle GFB is also double of the angle BFM. [[VI.
33]]
But the angle GFB is also double of the angle FAB, for
the angle FAB is equal to the angle ABF.
Therefore the angle BFN is also equal to the angle FAB.
But the angle ABF is common to the two triangles ABF
and BFN; therefore the remaining angle AFB is equal to the
remaining angle BNF; [[I. 32]] therefore the triangle
ABF
is equiangular with the triangle BFN.
Therefore, proportionally, as the straight line AB is to BF,
so is FB to BN; [[VI. 4]] therefore the
rectangle AB, BN is equal to the square on BF. [[VI.
17]]
Again, since AL is equal to LK, while LN is common
and at right angles, therefore the base KN is equal to the base
AN;
[[I. 4]] therefore the angle LKN is also equal
to the angle LAN.
But the angle LAN is equal to the angle KBN; therefore
the angle LKN is also equal to the angle KBN.
And the angle at A is common to the two triangles AKB
and AKN.
Therefore the remaining angle AKB is equal to the remaining
angle KNA; [[I. 32]] therefore the triangle KBA
is equiangular with the triangle KNA.
Therefore, proportionally, as the straight line BA is to AK,
so is KA to AN; [[VI. 4]] therefore the
rectangle BA, AN is equal to the square on AK. [[VI.
17]]
But the rectangle AB, BN was also proved equal to the
square on BF; therefore the rectangle AB, BN together
with the rectangle BA, AN, that is, the square on BA
[[II. 2]], is equal to the square on BF together
with the square on AK.
And BA is a side of the pentagon,
BF
of the hexagon [[IV. 15, Por.]], and AK of
the decagon.
Therefore etc. Q. E. D.
Euclid Elements 13.11 (Heath)
Illustrations courtesy of David E. Joyce
If in a circle which has its diameter rational an equilateral pentagon
be inscribed, the side of the pentagon
is the irrational straight line called minor.
For in the circle ABCDE which has its diameter rational let
the equilateral pentagon ABCDE
be inscribed; I say that the side of the pentagon
is the irrational straight line called minor.
For let the centre of the circle, the point F, be taken, let
AF,
FB
be joined and carried through to the points, G,
H, let AC
be joined, and let FK be made a fourth part of AF.
Now AF is rational; therefore FK is also rational.
But BF is also rational; therefore the whole BK is rational.
And, since the circumference ACG is equal to the circumference
ADG,
and in them ABC is equal to AED, therefore the remainder
CG
is equal to the remainder GD.
And, if we join AD, we conclude that the angles at L
are right, and CD is double of CL.
For the same reason the angles at M are also right, and AC
is double of CM. 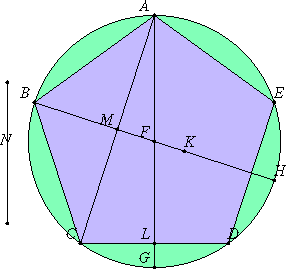
Since then the angle ALC is equal to the angle AMF, and
the angle LAC is common to the two triangles ACL and AMF,
therefore the remaining angle ACL is equal to the remaining angle
MFA;
[[I. 32]] therefore the triangle ACL is equiangular
with the triangle AMF; therefore, proportionally, as LC is
to CA, so is MF to FA.
And the doubles of the antecedents may be taken; therefore, as the
double of LC is to CA, so is the double of MF to FA.
But, as the double of MF is to FA, so is MF to
the half of FA; therefore also, as the double of LC is to
CA,
so is MF to the half of FA.
And the halves of the consequents may be taken; therefore, as the double
of LC is to the half of CA, so is MF to the fourth
of FA.
And DC is double of LC, CM is half of CA,
and FK a fourth part of FA; therefore, as DC is to
CM,
so is MF to FK.
Componendo also, as the sum of DC, CM is to CM,
so is MK to KF; [[V. 18]] therefore also,
as the square on the sum of DC, CM is to the square on CM,
so is the square on MK to the square on KF.
And since, when the straight line subtending two sides of the pentagon,
as AC, is cut in extreme and mean ratio, the greater segment is
equal to the side of the pentagon,
that is, to DC, [[XIII. 8]] while the square on
the greater segment added to the half of the whole is five times the square
on the half of the whole, [[XIII. 1]] and CM is
half of the whole AC, therefore the square on DC, CM
taken as one straight line is five times the square on CM.
But it was proved that, as the square on DC, CM taken
as one straight line is to the square on CM, so is the square on
MK
to the square on KF; therefore the square on MK is five times
the square on KF.
But the square on KF is rational, for the diameter is rational;
therefore the square on MK is also rational; therefore MK
is rational
And, since BF is quadruple of FK, therefore BK
is five times KF; therefore the square on BK is twenty-five
times the square on KF.
But the square on MK is five times the square on KF;
therefore the square on BK is five times the square on KM;
therefore the square on BK has not to the square on KM the
ratio which a square number has to a square number; therefore BK
is incommensurable in length with KM. [[X. 9]]
And each of them is rational.
Therefore BK, KM are rational straight lines commensurable
in square only.
But, if from a rational straight line there be subtracted a rational
straight line which is commensurable with the whole in square only, the
remainder is irrational, namely an apotome; therefore MB is an apotome
and MK the annex to it. [[X. 73]]
I say next that MB is also a fourth apotome.
Let the square on N be equal to that by which the square on
BK
is greater than the square on KM; therefore the square on BK
is greater than the square on KM by the square on N.
And, since KF is commensurable with FB, componendo also,
KB
is commensurable with FB. [[X. 15]]
But BF is commensurable with BH; therefore BK
is also commensurable with BH. [[X. 12]]
And, since the square on BK is five times the square on KM,
therefore the square on BK has to the square on KM the ratio
which 5 has to 1.
Therefore, convertendo, the square on BK has to the square on
N
the ratio which 5 has to 4 [[V. 19, Por.]], and
this is not the ratio which a square number has to a square number; therefore
BK
is incommensurable with N; [[X. 9]] therefore
the square on BK is greater than the square on
KM by the
square on a straight line incommensurable with BK.
Since then the square on the whole BK is greater than the square
on the annex KM by the square on a straight line incommensurable
with BK, and the whole BK is commensurable with the rational
straight line, BH, set out, therefore MB is a fourth apotome.
[[X. Deff. III. 4]]
But the rectangle contained by a rational straight line and a fourth
apotome is irrational, and its square root is irrational, and is called
minor. [[X. 94]]
But the square on AB is equal to the rectangle HB, BM,
because, when AH is joined, the triangle ABH is equiangular
with the triangle ABM, and, as HB is to BA, so is
AB
to BM.
Therefore the side AB of the pentagon
is the irrational straight line called minor. Q. E. D.
Euclid Elements 13.16 (Heath)
Illustrations courtesy of David E. Joyce
To construct an icosahedron and comprehend
it in a sphere,
like the
aforesaid figures; and to prove that the side of the icosahedron is the
irrational straight line called minor.
Let the diameter AB of the given sphere be set out, and let
it be cut at C so that AC is quadruple of CB, let
the semicircle ADB be described on AB, let the straight line
CD
be drawn from C at right angles
to AB, and let
DB be joined;  let the circle EFGHK be set out and let its radius be equal to DB,
let the equilateral and equiangular pentagonEFGHK
be inscribed in the circle EFGHK, let the circumferences
EF,
FG,
GH,
HK,
KE be bisected at the points L,
M,
N,
O,
P, and let LM,
MN, NO,
OP,
PL,
EP
be joined.
let the circle EFGHK be set out and let its radius be equal to DB,
let the equilateral and equiangular pentagonEFGHK
be inscribed in the circle EFGHK, let the circumferences
EF,
FG,
GH,
HK,
KE be bisected at the points L,
M,
N,
O,
P, and let LM,
MN, NO,
OP,
PL,
EP
be joined.
Therefore the pentagon LMNOP
is also equilateral, and the straight line EP belongs to a decagon.
Now from the points E, F, G, H, K
let the straight lines EQ, FR, GS, HT, KU
be set up at right angles to the plane of the circle, and let them be equal
to the radius of the circle EFGHK, let QR, RS, ST,
TU,
UQ,
QL,
LR,
RM, MS, SN,
NT,
TO,
OU,
UP,
PQ be joined.
Now, since each of the straight lines EQ, KU is at right
angles to the same plane, therefore EQ is parallel to KU.
[[XI. 6]]
But it is also equal to it; and the straight lines joining those extremities
of equal and parallel straight lines which are in the same direction are
equal and parallel. [[I. 33]]
Therefore QU is equal and parallel to EK.
But EK belongs to an equilateral pentagon;
therefore QU also belongs to the equilateral pentagon
inscribed in the circle EFGHK.
For the same reason each of the straight lines QR, RS,
ST,
TU
also belongs to the equilateral pentagon
inscribed in the circle EFGHK; therefore the pentagonQRSTU
is equilateral.
And, since QE belongs to a hexagon, and EP to a decagon,
and the angle QEP is right, therefore QP belongs to a pentagon;
for the square on the side of the pentagon
is equal to the square on the side of the hexagon and the square on the
side of the decagon inscribed in the same circle. [[XIII.
10]]
For the same reason PU is also a side of a pentagon.
But QU also belongs to a pentagon;
therefore the triangle QPU is equilateral.
For the same reason each of the triangles QLR, RMS, SNT,
TOU
is also equilateral.
And, since each of the straight lines QL, QP was proved
to belong to a pentagon, and LP
also belongs to a pentagon, therefore
the triangle
QLP is equilateral.
For the same reason each of the triangles LRM, MSN, NTO,
OUP
is also equilateral.
Let the centre of the circle EFGHK the point V, be taken;
from V let VZ be set up at right angles to the plane of the
circle, let it be produced in the other direction, as VX, let there
be cut off VW, the side of a hexagon, and each of the straight lines
VX,
WZ,
being sides of a decagon, and let QZ, QW,
UZ,
EV,
LV,
LX,
XM be joined.
Now, since each of the straight lines VW, QE is at right
angles to the plane of the circle, therefore VW is parallel to QE.
[[XI. 6]]
But they are also equal; therefore EV, QW are also equal
and parallel. [[I. 33]]
But EV belongs to a hexagon; therefore QW also belongs
to a hexagon.
And, since QW belongs to a hexagon, and WZ to a decagon,
and the angle QWZ is right, therefore QZ belongs to a pentagon.
[[XIII. 10]]
For the same reason UZ also belongs to a pentagon,
inasmuch as, if we join VK, WU, they will be equal and opposite,
and VK, being a radius, belongs to a hexagon; [[IV.
15, Por.]] therefore WU also belongs to a hexagon.
But WZ belongs to a decagon, and the angle UWZ is right;
therefore UZ belongs to a pentagon.
[[XIII. 10]]
But QU also belongs to a pentagon;
therefore the triangle QUZ is equilateral.
For the same reason each of the remaining triangles of which the straight
lines QR, RS, ST, TU are the bases, and the
point Z the vertex, is also equilateral.
Again, since VL belongs to a hexagon, and VX to a decagon,
and the angle LVX is right, therefore LX belongs to a pentagon.
[[XIII. 10]]
For the same reason, if we join MV, which belongs to a hexagon,
MX
is also inferred to belong to a pentagon.
But LM also belongs to a pentagon;
therefore the triangle LMX is equilateral.
Similarly it can be proved that each of the remaining triangles of
which MN, NO, OP, PL are the bases, and the
point X the vertex, is also equilateral.
Therefore an icosahedron has
been constructed which is contained by twenty equilateral triangles.
It is next required to comprehend it in the given sphere,
and to prove that the side of the icosahedron
is the irrational straight line called minor.
For, since VW belongs to a hexagon, and WZ to a decagon,
therefore VZ has been cut in extreme and mean ratio at W,
and VW is its greater segment; [[XIII. 9]] therefore,
as ZV is to VW, so is VW to WZ.
But VW is equal to VE, and WZ to VX; therefore,
as ZV is to VE, so is EV to VX.
And the angles ZVE, EVX are right; therefore, if we join
the straight line EZ, the angle XEZ will be right because
of the similarity of the triangles XEZ, VEZ.
For the same reason, since, as ZV is to VW, so is VW
to WZ, and ZV is equal to XW, and VW to WQ,
therefore, as XW is to WQ, so is QW to WZ.
And for this reason again, if we join QX, the angle at Q
will be right; [[VI. 8]] therefore the semicircle described
on XZ will also pass through Q. [[III. 31]]
And if, XZ remaining fixed, the semicircle be carried round
and restored to the same position from which it began to be moved, it will
also pass through Q and the remaining angular points of the icosahedron,
and the icosahedron will have been
comprehended in a sphere.
I say next that it is also comprehended in the given sphere.
For let VW be bisected at A'.
Then, since the straight line VZ has been cut in extreme and
mean ratio at W, and ZW is its lesser segment, therefore
the square on ZW added to the half of the greater segment, that
is WA', is five times the square on the half of the greater segment;
[[XIII. 3]] therefore the square on ZA' is five
times the square on A'W.
And ZX is double of ZA', and VW double of A'W;
therefore the square on ZX is five times the square on WV.
And, since AC is quadruple of CB, therefore AB
is five times BC.
But, as AB is to BC, so is the square on AB to
the square on BD; [[VI. 8], [V.
Def. 9]] therefore the square on AB is five times the square
on BD.
But the square on ZX was also proved to be five times the square
on VW.
And DB is equal to VW, for each of them is equal to the
radius of the circle EFGHK; therefore AB is also equal to
XZ.
And AB is the diameter of the given sphere;
therefore XZ is also equal to the diameter of the given sphere.
Therefore the icosahedron has
been comprehended in the given sphere
I say next that the side of the icosahedron
is the irrational straight line called minor.
For, since the diameter of the sphere is rational, and the square on
it is five times the square on the radius of the circle EFGHK, therefore
the radius of the circle EFGHK is also rational; hence its diameter
is also rational.
But, if an equilateral pentagon
be inscribed in a circle which has its diameter rational, the side of the
pentagon is the irrational straight
line called minor. [[XIII. 11]]
And the side of the pentagon
EFGHK is the side of the icosahedron.
Therefore the side of the icosahedron
is the irrational straight line called minor.
Euclid Elements 13.18 (Heath)
Illustrations courtesy of David E. Joyce
To set out the sides of the five figures and to compare them with one
another.
Let AB, the diameter of the given sphere, be set out, and let
it be cut at C so that AC is equal to CB, and at D
so that AD is double of DB; let the semicircle AEB
be described on AB, from C, D let CE, DF
be drawn at right angles to AB, and let AF, FB, EB
be joined.
Then, since AD is double of DB, therefore AB is
triple of BD. 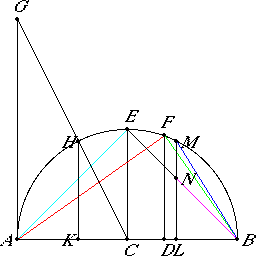
Convertendo, therefore, BA is one and a half times AD.
But, as BA is to AD, so is the square on BA to
the square on AF, [[V. Def. 9], [VI.
8]] for the triangle AFB is equiangular with the triangle AFD;
therefore the square on BA is one and a half times the square on
AF.
But the square on the diameter of the sphere is also one and a half
times the square on the side of the pyramid.
[[XIII. 13]]
And AB is the diameter of the sphere; therefore AF is
equal to the side of the pyramid.
Again, since AD is double of DB, therefore AB
is triple of BD.
But, as AB is to BD, so is the square on AB to
the square on BF; [[VI. 8], [V.
Def. 9]] therefore the square on AB is triple of the square
on BF.
But the square on the diameter of the sphere is also triple of the
square on the side of the cube.
[[XIII. 15]]
And AB is the diameter of the sphere; therefore BF is
the side of the cube.
And, since AC is equal to CB, therefore AB is
double of BC.
But, as AB is to BC, so is the square on AB to
the square on BE; therefore the square on AB is double of
the square on BE.
But the square on the diameter of the sphere is also double of the
square on the side of the octahedron.
[[XIII. 14]]
And AB is the diameter of the given sphere; therefore BE
is the side of the octahedron.
Next, let AG be drawn from the point A at right angles
to the straight line AB, let AG be made equal to AB,
let GC be joined, and from H let HK be drawn perpendicular
to AB.
Then, since GA is double of AC, for GA is equal
to AB, and, as GA is to AC, so is HK to KC,
therefore HK is also double of KC.
Therefore the square on HK is quadruple of the square on KC;
therefore the squares on HK, KC, that is, the square on HC,
is five times the square on KC.
But HC is equal to CB; therefore the square on BC
is five times the square on CK.
And, since AB is double of CB, and, in them, AD
is double of DB, therefore the remainder BD is double of
the remainder DC.
Therefore BC is triple of CD; therefore the square on
BC
is nine times the square on CD.
But the square on BC is five times the square on CK;
therefore the square on CK is greater than the square on CD;
therefore CK is greater than CD.
Let CL be made equal to CK, from L let LM
be drawn at right angles to AB, and let MB be joined.
Now, since the square on BC is five times the square on CK,
and AB is double of BC, and KL double of CK,
therefore the square on AB is five times the square on KL.
But the square on the diameter of the sphere is also five times the
square on the radius of the circle from which the icosahedron
has been described. [[XIII. 16, Por.]]
And AB is the diameter of the sphere; therefore KL is
the radius of the circle from which the icosahedron
has been described; therefore KL is a side of the hexagon in the
said circle. [[IV. 15, Por.]]
And, since the diameter of the sphere is made up of the side of the
hexagon and two of the sides of the decagon inscribed in the same circle,
[[XIII. 16, Por.]] and AB is the diameter
of the sphere, while KL is a side of the hexagon, and AK
is equal to LB, therefore each of the straight lines AK,
LB
is a side of the decagon inscribed in the circle from which the icosahedron
has been described.
And, since LB belongs to a decagon, and ML to a hexagon,
for ML is equal to KL, since it is also equal to HK,
being the same distance from the centre, and each of the straight lines
HK,
KL
is double of KC, therefore MB belongs to a pentagon.
[[XIII. 10]]
But the side of the pentagon
is the side of the icosahedron; [[XIII.
16]] therefore MB belongs to the icosahedron.
Now, since FB is a side of the cube,
let it be cut in extreme and mean ratio at N, and let NB
be the greater segment; therefore
NB is a side of the dodecahedron.
[[XIII. 17, Por.]]
And, since the square on the diameter of the sphere was proved to be
one and a half times the square on the side AF of the pyramid,
double of the square on the side BE of the octahedron
and triple of the side FB of the cube,
therefore, of parts of which the square on the diameter of the sphere contains
six, the square on the side of the pyramid
contains four, the square on the side of the octahedron
three, and the square on the side of the cube
two.
Therefore the square on the side of the pyramid
is fourthirds of the square on the side of the octahedron,
and double of the square on the side of the cube;
and the square on the side of the octahedron
is one and a half times the square on the side of the cube.
The said sides, therefore, of the three figures, I mean the pyramid,
the octahedron and the cube,
are to one another in rational ratios.
But the remaining two, I mean the side of the icosahedron
and the side of the dodecahedron, are not
in rational ratios either to one another or to the aforesaid sides; for
they are irrational, the one being minor [[XIII. 16]]
and the other an apotome [[XIII. 17]].
That the side MB of the icosahedron
is greater than the side
NB of the dodecahedron
we can prove thus.
For, since the triangle FDB is equiangular with the triangle
FAB,
[[VI. 8]] proportionally, as DB is to BF,
so is BF to BA. [[VI. 4]]
And, since the three straight lines are proportional, as the first
is to the third, so is the square on the first to the square on the second;
[[V. Def. 9], [VI. 20, Por.]]
therefore, as DB is to BA, so is the square on DB
to the square on BF; therefore, inversely, as AB is to BD,
so is the square on FB to the square on BD.
But AB is triple of BD; therefore the square on FB
is triple of the square on BD.
But the square on AD is also quadruple of the square on DB,
for AD is double of DB; therefore the square on AD
is greater than the square on FB; therefore AD is greater
than FB; therefore AL is by far greater than FB.
And, when AL is cut in extreme and mean ratio, KL is
the greater segment, inasmuch as LK belongs to a hexagon, and KA
to a decagon; [[XIII. 9]] and, when FB is cut
in extreme and mean ratio, NB is the greater segment; therefore
KL
is greater than NB.
But KL is equal to LM; therefore LM is greater
than NB.
Therefore MB, which is a side of the icosahedron,
is by far greater than NB which is a side of the dodecahedron.
Q. E. D.
I say next that no other figure, besides the said five figures,
can
be constructed which is contained by equilateral and equiangular figures
equal to one another.
For a solid angle cannot be constructed with two triangles, or indeed
planes.
With three triangles the angle of the pyramid
is constructed, with four the angle of the octahedron,
and with five the angle of the icosahedron; but a solid angle cannot be
formed by six equilateral and equiangular triangles placed together at
one point, for, the angle of the equilateral triangle being two-thirds
of a right angle, the six will be equal to four right angles: which is
impossible, for any solid angle is contained by angles less than four right
angles. [[XI. 21]]
For the same reason, neither can a solid angle be constructed by more
than six plane angles.
By three squares the angle of the cube
is contained, but by four it is impossible for a solid angle to be contained,
for they will again be four right angles.
By three equilateral and equiangular pentagons the angle of the dodecahedron
is contained; but by four such it is impossible for any solid angle to
be contained, for, the angle of the equilateral pentagon
being a right angle and a fifth, the four angles will be greater than four
right angles: which is impossible.
Neither again will a solid angle be contained by other polygonal figures
by reason of the same absurdity.
Therefore etc. Q. E. D.
Go to page: 1; 2