Caspar & Fontano

Consulter ce site en ligne

Autorisation

Pavages sur www

Pavages

 

ABSTRACT

DISCUSSION

Graphics methods.

Pentilings.

Crystalline eta Phase Alloys.

Kepler's Pentagon Tiling.

Pentangulation.

Fibonacci Pentilings.

Reordering Pentilings.

Diffraction Patterns and Patterson Functions.

Quasicrystal Crystallography.

Decagonal Quasicrystal Structures.

Conclusion.

FIGURES

FIG. 1. Dürer's pentilings.

FIG. 2. Projected electron density map of FeAl₃  eta phase alloy and superimposed P₀ = 2 pentile lattice.

FIG. 3. Kepler's tiling with pentagons and decagons and a P = 34 pentiling generated from Kepler's matrix.

FIG. 4. Iterative pentangulation of the P₀ = 2 pentiling.

FIG. 5. Periodic pentilings with more than two pentagons per unit cell.

FIG. 6. Superposition of Kepler's and Penrose's pentagon tilings.

FIG. 7. Diffraction patterns of regular pentilings.

FIG. 8. Patterson maps of regular pentilings.

FIG. 9. Embellished P₈ = 89 Patterson map from Fig. 8.

FIG. 10. Indexing of the P₈ = 89 diffraction pattern.

REFERENCES

 This paper was presented at a colloquium entitled "Symmetries Throughout the Sciences," organized by Ernest Hendley, held May 11 and 12, 1996, at the National Academy of Sciences in Irvine, CA.

Five-fold symmetry in crystalline quasicrystal lattices

DONALD L. D. CASPAR AND ERIC FONTANO

Institute of Molecular Biophysics, Florida State University, Tallahassee FL 32306-4380

ABSTRACT     To demonstrate that crystallographic methods can be applied to index and interpret diffraction patterns from well-ordered quasicrystals that display non-crystallographic five-fold symmetry, we have characterized the properties of a series of periodic two-dimensional lattices built from pentagons, called Fibonacci pentilings, which resemble aperiodic Penrose tilings. The computed diffraction patterns from periodic pentilings with moderate size unit cells show decagonal symmetry and are virtually indistinguishable from that of the infinite aperiodic pentiling. We identify the vertices and centers of the pentagons forming the pentiling with the positions of transition metal atoms projected on the plane perpendicular to the decagonal axis of quasicrystals whose structure is related to crystalline eta phase alloys. The characteristic length scale of the pentiling lattices, evident from the Patterson (autocorrelation) function, is ~ t² times the pentagon edge length, where t is the golden ratio. Within this distance, there are a finite number of local atomic motifs whose structure can be crystallographically refined against the experimentally measured diffraction data. 

     Quasicrystallography has developed into an elaborate discipline since 1984 when Shechtman et al. (4) first reported crystal-like diffraction patterns with forbidden icosahedral symmetry from aluminum-manganese alloys, and Levine and Steinhardt (5) coined the name quasicrystals for the class of quasiperiodic structures. Exposition of the results of many experimental studies on these novel alloys, and of the efforts of physicists to model their properties are presented in the book Quasicrystals: a primer by Janot (6); and the mathematical concepts involved in the construction of aperiodic lattices are described in Quasicrystals and geometry, by Senechal (2).

     In their endeavors, quasicrystallographers have utilized a variety of mathematically sophisticated but physically unrealistic models to analyze aperiodic lattices with icosahedral or decagonal symmetry. Quasicrystal structures have been represented as projections into two- or three-dimensional space from periodic models in five- or six-dimensional space. For example, such procedures have been applied by Steurer and his colleagues to calculate five-dimensional Fourier maps from three-dimensional X-ray diffraction patterns of decagonal phase aluminum-transition metal alloy quasicrystals (7,8,9). Projections from these physically abstract five-dimensional constructs produce real space maps which show correlations with the crystallographically-determined atomic arrangements in related periodically ordered alloys (10,11,12). The success of this five-dimensional quasicrystallographic analysis suggests that, because the diffraction data is only observable in three-dimensional reciprocal space, more conventional crystallographic analysis might be applied to refine real space models of the atomic arrangements in these quasicrystals.

     Quasicrystals are, by definition, aperiodic lattices. The diffraction pattern from one portion of such a lattice is indistinguishable from that of another portion. A representative portion of a quasicrystal lattice can be chosen as a large unit cell of a perfectly periodic lattice that would yield the same diffraction pattern as the aperiodic lattice. A great variety of such periodic lattices can be constructed by selecting different portions of the aperiodic lattice as the unit cell. The fact that such lattices exist suggests that one member of this class might be transformed into any other member by localized displacive rearrangements of the constituent atoms.

     Our surmise is that quasicrystals with icosahedral or decagonal symmetry may be modeled by periodic packing arrangements of icosahedra or pentagons in moderate-size unit cells that can be locally rearranged, conserving key bonding relations, to generate aperiodic lattices. In this paper, we focus consideration on regular arrangements of pentagons in the plane, applying the same sort of packing rules as used by Dürer (13), Kepler (1) and Penrose (3) in their explorations of pentagonal tilings. The designs of these regular pentagonal tilings are related to the arrangement of transition metal atoms projected on the plane perpendicular to the axes of local five-fold symmetry in the alloys with aluminum of the crystallographically regular eta phase (10,11,12) and the decagonal quasicrystals (7,8).

     Graphics methods. To visualize the regular arrangements of pentagons (pentilings), their relation to crystal structures, quasicrystal diffraction patterns and Patterson functions, special purpose graphics routines were developed. All images were created and rendered using unique code in the PostScript language (14). Pentilings were created using recursive routines, and coordinates needed for Fourier analyses were generated from the PostScript code using the Aladdin Ghostscript interpreter. Once in PDB format, the coordinates were used with the CCP4 package (15) to calculate electron density maps, structure factors and Patterson maps. The maps were converted to grayscale images and then embedded in PostScript documents. The construction of twinned lattice images and montages utilized the PostScript clipping and superposition capabilities.

     Pentilings. We define a pentiling as an arrangement of regular pentagons in the plane in which each pentagon makes edge-to-edge contact with two, three, four or five neighbors, thereby sharing vertices in such a way that no gaps large enough to contain another pentagon are left in the array. A periodic pentiling is a regular lattice with P pentagons in the unit cell. P is called the pentile number.
 
 

FIG. 1: Dürer's pentilings. (a) The repeating unit of the P₀ = 2 pentiling consists of two pentagons (orange) and one lozenge gap arranged with c2mm plane group symmetry. The primitive unit cell is marked by solid lines or dashed lines in the alternate lozenge shape. The pair of 36° wedge regions, comprising a fifth of the pentile lattice, was used to construct the pentagonally twinned lattice (b) by applying five-fold rotation symmetry about the central pentagon. The twinning of the P₀ = 2 pentiling does not alter the local coordination pattern marked by dotted lines. The ten boundary twinning lines mark rows of pentagons that are shared by neighboring P₀ = 2 lattice domains oriented at 36° to each other. The orange pentagons simulate Dürer's twinning pattern (13).

     Crystalline eta Phase Alloys.

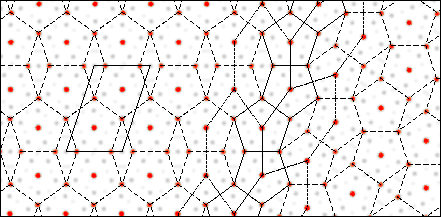
FIG. 2: Projected electron density map of FeAl₃ eta phase alloy and superimposed P₀ = 2 pentile lattice. The density map was constructed from the atomic coordinates (10), applying a temperature factor of 5 Ų to all atoms and projecting the density on the plane perpendicular to the monoclinic b axis. The twinning was modeled by rotating a portion of the map by 36° and rejoining as illustrated in Fig. 1b. The regular P₀ = 2 pentiling, marked by the dashed lines, closely fits the map with the iron atoms located at the vertices and centers of the pentagons of mean edge length E = 4.78 Å. The common set of pentagons at the twinning boundary is marked by solid lines, with portions of the pattern connecting pentagon centers on either side of the boundary indicated by fine dashed lines.

     Kepler's Pentagon Tiling. Consideration of Kepler's orderly arrangements of pentagons (1) led to insight into ways in which periodic pentilings may be aperiodically disordered. Kepler's tiling with pentagons and decagons from Fig. Aa of his Harmonices Mundi Book II is shown in a computer graphics facsimile in Fig. 3a. Senechal (2) considered this a nonrepeating pattern and concluded that Penrose's first pentagonal tiling family (3) (cf. Fig. 6) is essentially a completion of Kepler's Fig. Aa. In his description of the procedure he used to combine pentagons and decagons in this figure, Kepler commented: "If you really wish to continue the pattern, certain irregularities must be admitted, two decagons must be combined ... . So as it progresses this five-cornered pattern continually introduces something new." However, examination of his pattern shows that a basic repeating unit can be outlined by connecting the star centers to form the elongated hexagons marked in Fig. 3a. These hexagon units have exactly the same shape and packing arrangement as those formed by connecting the pentagon centers in Fig. 1b of Dürer's perfect pentagonal twinning of the P₀ = 2 pentiling. Adding pentagons to extend the regular pattern of Kepler's tiling, we can say with Dürer: "You can continue in this manner as long as you desire."

     Kepler's repeating unit can be assembled into a lattice with perfectly regular translational symmetry, as shown in Fig. 3b. Each decagonal cavity can be fitted with three pentagons and each pair of fused pentagons with six. This completed tiling has pentile number P = 34. The three pentagons in each decagon can be placed in 10 different orientations conserving the number of possible edge-to-edge contacts. There are 52 ways in which the six pentagons can be fitted into the fused decagon pair conserving edge-to-edge contacts. (There are 12 more ways that these pentagons can be fitted without overlap which sacrifice an edge-to-edge contact, but these are excluded by our local packing rule for optimizing contacts.) Therefore, there are 5,200 ways in which 12 pentagons can be added to Kepler's 22 pentagon matrix to conserve the number of contacts and packing density (There are, however, only 1,314 combinations with non-identical autocorrelation functions, counting up-down and enantiomorphic pairs only once.) The pentagons forming Kepler's matrix can also be conservatively reoriented. For example, the five pentagons bordering each pentagram can be flipped in 15 different combinations. Thus, there are an extremely large number of isomers of the P = 34 pentiling, and a larger number of ways in which any of these regular lattices can be discretely disordered, conserving the number of contacts and packing density.

     It is evident that the transition metal atoms in the eta phase alloys could be arrayed in pentagonal columns corresponding to the pentagons of any of the isomeric or discretely disordered P = 34 pentilings, conserving very similar local packing arrangements. Our surmise is that all the isomers and discretely disordered versions of the P = 34 pentiling just described will have very similar autocorrelation functions, and therefore similar diffraction patterns. We will compare diffraction patterns and Patterson (autocorrelation) functions of different pentilings after more systematic analysis of their designs and packing properties.

FIG. 3: (a) Kepler's tiling with pentagons and decagons (1) and (b) a P = 34 pentiling generated from Kepler's matrix. The pattern formed by connecting the pentagrams in (a) can be continued indefinitely, as in Fig. 1b, to construct a perfect pentagonal twin of the elongated hexagonal units comprised of 22 pentagons, two decagons, two fused decagons and two pentagrams. By arranging Kepler's matrix unit with translational symmetry and filling the decagonal spaces with twelve pentagons, a regular P = 34 pentiling is formed in (b). Flipping some pentagons at random will produce an aperiodic tiling.

      Pentangulation. How can the possible periodic pentilings with P > 2 be systematically enumerated? An obvious strategy is that used by Penrose (3) to generate aperiodic tilings with pentagons: starting with a pentagonal array of pentagons, each pentagon was subdivided into six smaller pentagons and the gaps in the array between the larger pentagons were filled with the smaller ones; and this process was iterated. Geometers call this process substitution tiling (2). In our application of this substitution tiling strategy to enumerate periodic pentilings, we call the process pentangulation by analogy with the triangulation process used to enumerate possible icosahedral surface lattice designs in the quasiequivalence theory of icosahedral virus construction (19).

FIG. 4: Iterative pentangulation of the P₀ = 2 pentiling. In the basic pentangulation process (a), six small pentagons are fit into each of the two larger pentagons of the P₀ = 2 pentiling and a single small pentagon is fit into the lozenge gap to generate the P₄ = 13 pentiling. The repeating unit of P₄ = 13 comprises 13 pentagon centers, 29 pentagon vertices, one pentagram, one trigram and three lozenge gaps. Because five small pentagons fit in the pentagram gap and three fit in the trigram gap, the next stage of pentangulation (b) generates P₈ = 6 ? 13 + 5 ? 1 + 3 ? 1 + 1 ? 3 = 89 pentagons. Continuing this process (c), pentangulation of P₈ = 89 generates P₁₂ = 610.

     Fibonacci Pentilings. The fact that the pentangulations of P₀ = 2 generate a fourth order sequence of Fibonacci pentile numbers, and the P = 34 pentiling generated from Kepler's net represents another Fibonacci pentile number, suggests that the sequence of pentilings with P_n = F_n+3 may be particularly relevant for characterizing the geometry of decagonal quasicrystals.

FIG. 5: Periodic pentilings with more than two pentagons per unit cell. Pentagons in a repeating unit are orange and unit cells are marked by solid lines. The regular Fibonacci pentilings P₀ = 2, P₁ = 3, P₂ = 5 and P₃ = 8 are the first four members of the series listed in Table 1 whose pentagon packing densities are approximately t/2. As explained in the text, the two versions of P = 4 illustrated have packing densities that differ significantly from that of the closest Fibonacci pentilings (P₁ = 3 and P₂ = 5). Different pentiling lattices can be twinned with themselves or each other in various combinations. P = 4a corresponds to periodic twinning of P₀ = 2. The illustrated twinning of P₂ = 5 and P₃ = 8, with the common boundary marked, exemplifies one of the many ways in which periodic pentilings can be combined to generate less regular pentilings.
 

     Reordering Pentilings. The larger the pentile number, the larger the number of isomers and the greater the possibilities for introducing discrete disorder by flipping pentagons without altering the mean coordination or packing density (cf. Fig. 3b). Such local displacive rearrangements can also transform one ordered pentiling into another with comparable packing density. Fig. 6 illustrates the superposition of Kepler's pentagonally-twinned matrix of pentagons (from Fig. 3a) on the first "aperiodic" tiling presented by Penrose (3). Penrose's tiling can be represented as the second pentangulation of Dürer's (13) pentagonally-twinned P₀ = 2 pentiling to generate the five-fold twin of the P₈ = 89 pentiling. The superposition in Fig. 6 requires 11 pentagon flips within the frame. There are many other ways in which Kepler's tiling, or regularly periodic versions of it, can be superimposed on Penrose's tiling that require different numbers of pentagon flips. These pentagon flips should correspond to energetically equivalent local packing arrangements.

     A pentagon flip in atomic terms corresponds to interchanging a pentagon center and vertex in one orientation for a vertex and center in the other. The displacement in the plane of the pentagon for the two sites is E tan 18°, which, if E = 4.7 Å, involves a lateral movement of 1.5 Å. In the eta phase alloys (10,12), the axial metal atoms sit ~ 1.7 Å above or below the pentagonal plane. Interchange of axial and vertex positions would involve coupled movements of ~ 2.3 Å. The activation energy for such coordinated movements in columns of atoms might be very high, but could be facilitated by lattice defects designated as phasons in quasicrystallography (6). Even if such flips are rare in the locally well-ordered condensed state, during crystallization columns of atoms would have to choose between pentagon axial and vertex sites. .

FIG. 6: Superposition of Kepler's and Penrose's pentagon tilings. Penrose's tiling (3), marked by the boldly outlined pentagons, is a perfect five-fold twin of the P₈ = 89 pentiling whose unit cells are marked by the portions of the lightly outlined 36° rhombs centered on the starred pentagon. This facsimile of his tiling has been extended 11% to the left of his margin to give the frame a golden aspect ratio. Kepler's pentagonally twinned matrix of shaded pentagons, from Fig. 3a, is centered on a pentagram in a region of Penrose's tiling that has only local five-fold symmetry. The 11 sites within this frame at which pentagon flips are necessary to transform from Penrose's to Kepler's pattern can be recognized by the shaded pentagons that do not match the bold outline. Kepler's matrix cells, outlined with dashes, each contain an isomer of the P₆ = 34 unit, which can be distinguished by the orientation of the twelve pentagons inside the decagonal spaces. Curiously, four of these cells contain the same isomer. The density of the P₆ = 34 pentiling is 0.0148% greater than that of P₈ = 89, amounting to one more pentagon in an area ~ 20? that shown here.

     Diffraction Patterns and Patterson Functions. "Atomic" models based on several of our Fibonacci pentilings were constructed by placing atoms at the centers and vertices of the pentagons. This construction for P₀ = 2 corresponds to omitting the aluminum atoms from the projected map of Black's (10) eta phase FeAl₃ structure in Fig. 2. A montage of the modeled diffraction patterns and Patterson functions for P₀ = 2, P₄ = 13, P₆ = 34 and P₈ = 89 are shown in Figs. 7 and 8. The arrangement of the pentagons in the P₀ = 2 pentiling has mm symmetry, and arrangements were chosen for the even order pentilings with a line of mirror symmetry perpendicular to the a axis (i.e., along the long axis of the 36° lozenge unit cell). Thus, the Fourier transforms have mm symmetry and the single quadrant displayed for each model in Fig. 7 represents all the diffraction data. The Patterson functions (Fig. 8), were calculated from the squared structure factors illust

FIG. 7: Diffraction patterns of regular pentilings. Model electron density maps similar to Fig. 2 were calculated by placing identical atoms with temperature factors of 5 Ų at the vertices and centers of pentagons in the P₀ = 2, P₄ = 13, P₆ = 34 and P₈ = 89 pentilings from Figs. 1a, 4a, 3b and 4b respectively. The pentagon edge length E in this construction is 4.7 Å. Fast Fourier transforms of these maps were calculated to 0.9 Å resolution and the amplitudes were scaled by setting F₀₀ to unity. The maximum scaled amplitude in each pattern is |F_max| ~ 0.2. The quadrants, which include all independent Fourier coefficients for each pattern, are aligned with the (0,k) axis horizontal. The patterns from the higher order pentilings have evident ten-fold symmetry. Comparison across the boundary between the P₆ = 34 and P₈ = 89 patterns demonstrates that they are virtually indistinguishable. The structure factors, which are discrete points in reciprocal space, are depicted as Gaussian disks with radii proportional to the amplitudes as indicated in the |F| scale at the top. The intensity range displayed is ~ 100.

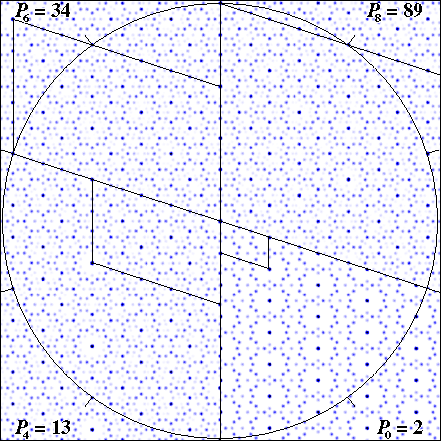
FIG. 8: Patterson maps of regular pentilings. Sectors of the four Patterson maps are aligned with their a axes vertical and their unit cells outlined (the b axis of P₈ = 89 extends beyond the image frame). The circle has radius 52.4 Å = t⁵E, which is equal to the a axis of P₈ = 89 and the b axis of P₆ = 34, and is marked every 36° to emphasize the ten-fold symmetry.

     Quasicrystal Crystallography.

FIG. 9: Embellished P₈ = 89 Patterson map from Fig. 8. Unit cell axes are marked and the a axis is vertical. The map has mirror symmetry parallel and perpendicular to the a axis at the origin and at a/2 marked with a cross. The centers of symmetry at the left and right margins are also marked. Circles of radius tE and t²E are drawn about the crystallographic origins. Circles of radius tE are drawn about the quasiequivalent origins related by the local noncrystallographic ten-fold axes and the crystallographic centers of symmetry. Circles of radius t²E can also be drawn around the quasiequivalent origins which fit like that about the crystallographic origin.

FIG. 10: Indexing of the P₈ = 89 diffraction pattern. The quadrant in Fig. 7 is enlarged and the most intense spots are labeled with their h,k indices. The thick lines, which are parallel to the crystal axes and are spaced at intervals of consecutive Fibonacci numbers, pass through rows of lattice points including the most intense spots. The thin lines, at angles of ±36° to the (0,k) direction, are noncrystallographic but nearly pass through centers of the intense spots related by the noncrystallographic ten-fold symmetry.

     Decagonal Quasicrystal Structures.       We thank Bin Yu for assistance with the crystallographic calculations. This work has been supported by a U. S. public health service research grant from the National Institutes of Health's National Cancer Institute, grant number CA47439-08. 

1. Kepler, J. (1619) Harmonices Mundi (Facsimile Edition: Forni Editore, Bologna (1969); Book II: On the congruence of harmonic figures. English translation by J. V. Field in Vistas in Astronomy 23, 109-141 (1979)).
2. Senechal, M. (1995) Quasicrystals and Geometry (Cambridge Univ. Press, Cambridge, U.K.).
3. Penrose, R. (1979) Math. Intelligencer 2, 32-37.
4. Shechtman, D., Blech, I., Gratias, D. & Cahn, J. W. (1984) Phys. Rev. Lett. 53, 1951-1953.
5. Levine, D. & Steinhardt, P. J. (1984) Phys. Rev. Lett. 53, 2477-2480.
6. Janot, C. (1992) Quasicrystals: a primer (Clarendon Press, Oxford, U.K.).
7. Steurer, W. & Kuo, K. H. (1990) Acta Cryst. B46, 703-712.
8. Steurer, W. Haibach, T., Zang, B. Kek, S. & Lück, R. (1993) Acta Cryst. B49, 661-675.
9. Haibach, T. & Steurer, W. (1996) Acta Cryst. A52, 277-286.
10. Black, P. J. (1955) Acta Cryst. 8, 43-48.
11. Black, P. J. (1955) Acta Cryst. 8, 175-181.
12. Hudd, R. C. & Taylor, W. H. (1962) Acta Cryst. 15, 441-442.
13. Dürer, A. (1525) A manual of measurement of lines, areas and solids by means of compass and ruler (Facsimile Edition translated with commentary by W. L. Strauss (1977), Abaris Books, Inc., New York).
14. Adobe Systems, Inc. (1990) PostScript Language Reference Manual, second edition (Addison-Wesley, Reading, MA).
15. Collaborative Computational Project Number 4 (1994) Acta Cryst.D50, 760-763.
16. Kiselev, N. A. & Klug, A. (1969) J. Mol. Biol. 40, 155-171.
17. Rayment, I., Baker, T. S., Caspar, D. L. D. & Murakami, W. T. (1982) Nature (London) 295, 110-115.
18. Salunke, D. M., Caspar, D. L. D. & Garcea, R. L. (1989) Biophys. J. 56, 887-900.
19. Caspar, D. L. D. & Klug, A. (1962) Cold Spring Harbor Symp. Quant. Biol. 27, 1-24.
20. Stephens, P. W. and Goldman, A. I. (1991) Sci. Amer. April, 44-53.
21. James, R. W. (1954) The Optical Principles of the Diffraction of X-rays (G. Bell and Sons, London).
22. Clarage, J. B., Clarage, M. S., Phillips, W. C., Sweet, R. M. and Caspar, D. L. D. (1992) Proteins 12, 145-157.
23. Hendrickson, W. A. & Konnert, J. H. (1981) Biomolecular Structure: Conformation, Function and Evolution, Vol. I, edited by R. Srinivasan, pp. 43-57 (Pergamon Press, Oxford, U.K.).
24. Brünger, A. T. (1990) X-PLOR Manual, Version 2.1 (Howard Hughes Medical Institute, Yale Univ., New Haven, CT). 

    ---

    Subject:

          Re: penrose tiling
    Date:
          Thu, 08 Oct 1998 17:02:18 -0500
   From:
          "Donald L. D. Caspar" <caspar@val.sb.fsu.edu>
      To:
          david.Boeno@wanadoo.fr
 

Dear M. Boeno,

I would be very pleased for you to include a link to my home page on
Fivefold Symmetry and Quasicrystals, and I would be very interested in
seeing your art show when you have it on the Internet.

With best wishes,

Don Caspar